Compilers Principles, Techniques, & Tools (purple dragon book) second edition exercise answers

Exercises for Section 3.9

3.9.1

Extend the table of Fig. 3.58 to include the operators

  1. ？
  2. +

Answer

node n nullable(n) firstpos(n)
n = c_1 ? true firstpos(c_1)
n = c_1 + nullable(c_1) firstpos(c_1)

3.9.2

Use Algorithm 3.36 to convert the regular expressions of Ex­ercise 3.7.3 directly to deterministic finite automata.

Answer

  1. (a|b)*

    • Syntax tree

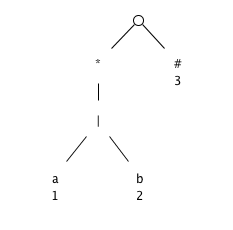
      3 9 2-1-1

    • firstpos and lastpos for nodes in the syntax tree

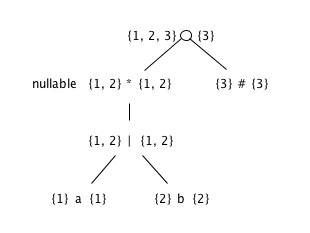
      3 9 2-1-2

- The function followpos

    <table>
        <thead>
            <tr>
                <th>node n</th>
                <th>followpos(n)</th>
            </tr>
        </thead>
        <tbody>
            <tr>
                <td>1</td>
                <td>{1, 2, 3}</td>
            </tr>
            <tr>
                <td>2</td>
                <td>{1, 2, 3}</td>
            </tr>
            <tr>
                <td>3</td>
                <td>∅</td>
            </tr>
        </tbody>
    </table>

  • Steps

    The value of firstpos for the root of the tree is {1, 2, 3}, so this set is the start state of D. Call this set of states A. We compute Dtran[A, a] and Dtran[A, b]. Among the positions of A, 1 correspond to a, while 2 correspond to b. Thus Dtran[A, a] = followpos(1) = {1, 2, 3}， Dtran[A, b] = followpos(2) = {1, 2, 3}. Both the results are set A, so dose not have new state, end the computation.

  • DFA

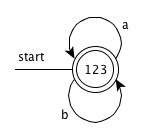
3 9 2-1-dfa

  1. (a*|b*)*

  2. ((ε|a)|b*)*

  3. (a|b)*abb(a|b)*

3.9.3 !

We can prove that two regular expressions are equivalent by showing that their minimum-state DFA's are the same up to renaming of states. Show in this way that the following regular expressions: (a|b)*, (a*|b*)*, and ((ε|a)b*)* are all equivalent. Note: You may have constructed the DFA's for these expressions in response to Exercise 3.7.3.

Answer

Refer to the answers of 3.7.3 and 3.9.2-1

3.9.4 !

Construct the minimum-state DFA's for the following regular expressions:

  1. (a|b)*a(a|b)
  2. (a|b)*a(a|b)(a|b)
  3. (a|b)*a(a|b)(a|b)(a|b)

Do you see a pattern?

3.9.5 !!

To make formal the informal claim of Example 3.25, show that any deterministic finite automaton for the regular expression

(a|b)*a(a|b)...(a|b)

where (a|b) appears n - 1 times at the end, must have at least 2n states. Hint: Observe the pattern in Exercise 3.9.4. What condition regarding the history of inputs does each state represent?