- Introduction
- 1. 1.Introduction
- 2. 2.A Simple Syntax-Directed Translator
- 3. 3.Lexical Analysis
- 4. 4.Syntax Analysis
- 5. 5.Syntax-Directed Translation
- 6. 6.Intermediate-Code Generation
- 7. 7.Run-Time Environments
- 8. 8.Code Generation
- 9. 12.InterProcedural Analysis
- Published with GitBook
第2章要点
1. 文法、语法制导翻译方案、语法制导的翻译器
以一个仅支持个位数加减法的表达式为例
文法
list -> list + digit | list - digit | digit
digit -> 0 | 1 | … | 9
(消除了左递归的)语法制导翻译方案
expr -> term rest
rest -> + term { print('+') } rest | - term { print('+') } rest | ε
term -> 0 { print('0') } | 1 { print('1') } | … | 9 { print('9') }
语法制导的翻译器
java代码见 p46
2. 语法树、语法分析树
以 2 + 5 - 9 为例
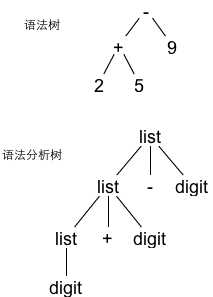
3. 正则文法、上下文无关文法、上下文相关文法?
文法缩写:
正则文法
正则文法在标准之后所有产生式都应该满足下面三种情形中的一种:
B -> a
B -> a C
B -> epsilon
关键点在于:
- 产生式的左手边必须是一个非终结符。
- 产生式的右手边可以什么都没有,可以有一个终结符,也可以有一个终结符加一个非终结符。
从产生式的角度看,这样的规定使得每应用一条产生规则,就可以产生出零或一个终结符,直到最后产生出我们要的那个字符串。
从匹配的角度看,这样的规定使得每应用一条规则,就可以消耗掉一个非终结符,直到整个字符串被匹配掉。
这样定义的语言所对应的自动机有一种性质:有限状态自动机。
简单来说就是只需要记录当前的一个状态,和得到下一个输入符号,就可以决定接下来的状态迁移。
正则文法和上下文无关文法
CFG 跟 RG 最大的区别就是,产生式的右手边可以有零或多个终结符或非终结符,顺序和个数都没限制。
想像一个经典例子,括号的配对匹配:
expr -> '(' expr ')' | epsilon
这个产生式里(先只看第一个子产生式),右手边有一个非终结符 expr,但它的左右两侧都有终结符,这种产生式无法被标准化为严格的 RG 。这就是CFG的一个例子。
它对应的自动机就不只要记录当前的一个状态,还得外加记录到达当前位置的历史,才可以根据下一个输入符号决定状态迁移。所谓的“历史”在这里就是存着已匹配规则的栈。
CFG 对应的自动机为 PDA(下推自动机)。
RG 的规定严格,对应的好处是它对应的自动机非常简单,所以可以用非常高效且简单的方式来实现。
上下文相关文法
CSG 在 CFG的基础上进一步放宽限制。
产生式的左手边也可以有终结符和非终结符。左手边的终结符就是“上下文”的来源。也就是说匹配的时候不能光看当前匹配到哪里了,还得看当前位置的左右到底有啥(也就是上下文是啥),上下文在这条规则应用的时候并不会被消耗掉,只是“看看”。
CSG 的再上一层是 PSG,phrase structure grammar。
基本上就是CSG的限制全部取消掉。
左右两边都可以有任意多个、任意顺序的终结符和非终结符。
反正不做自然语言处理的话也不会遇到这种文法,所以具体就不说了。
4. 为什么有 n 个运算符的优先级,就对应 n+1 个产生式?
优先级的处理可以在纯文法层面解决,也可以在parser实现中用别的办法处理掉。
纯文法层面书上介绍的,有多少个优先级就有那么多加1个产生式。
书上介绍的四则运算的文法,会使得加减法离根比较近,乘除法离根比较远。
语法树的形状决定了节点的计算顺序,离根远的节点就会先处理,这样看起来就是乘除法先计算,也就是乘除法的优先级更高。
参考:http://rednaxelafx.iteye.com/blog/492667
5. 避免二义性文法的有效原则?
二义性问题主要是跟 CFG 的特性有关系的。
CFG 的选择结构("|")是没有规定顺序或者说优先级的, 同时,多个规则可能会有共同前缀, 这样才会有二义性问题。
PEG 是跟CFG类似的一种东西,语言的表达力上跟CFG相似。 但文法层面没有二义性,因为它的选择结构("|")是有顺序或者说有优先级的。
6. 避免预测分析器因左递归文法造成的无限循环
产生式:
A -> A x | y
语法制导翻译伪代码片段:
void A(){
switch(lookahead){
case x:
A();match(x);break;
case y:
match(y):break;
default:
report("syntax error")
}
}
当语句符合 A x 形式时, A() 运算会陷入死循环,可以通过将产生式改为等价的非左递归形式来避免:
B -> y C
C -> x C | ε
7. 为什么在右递归的文法中,包含了左结合运算符的表达式翻译会比较困难?
8. 中间代码生成时的左值和右值问题。
看了书上 lvalue() 和 rvalue() 的伪代码,感觉可以做左值也可以做右值的都由 lvalue() 处理,而对于右值的处理,要么自己处理掉了,对于可以作为左值的右值则调用 lvalue()。
为什么不直接弄个 value() 就结了?