- Introduction
- 1. 1.Introduction
- 2. 2.A Simple Syntax-Directed Translator
- 3. 3.Lexical Analysis
- 4. 4.Syntax Analysis
- 5. 5.Syntax-Directed Translation
- 6. 6.Intermediate-Code Generation
- 7. 7.Run-Time Environments
- 8. 8.Code Generation
- 9. 12.InterProcedural Analysis
- Published with GitBook
3.6 Exercises for Section 3.6
3.6.1 !
Figure 3.19 in the exercises of Section 3.4 computes the failure function for the KMP algorithm. Show how, given that failure function, we can construct, from a keyword b1b2...bn an n + 1-state DFA that recognizes .*b1b2...bn, where the dot stands for "any character." Moreover, this DFA can be constructed in O(n) time.
Answer
Take the string "abbaabb" in exercise 3.4.3-3 as example, the failure function is:
- n : 1, 2, 3, 4, 5, 6, 7
- f(n): 0, 0, 0, 1, 1, 2, 3
The DFA is:
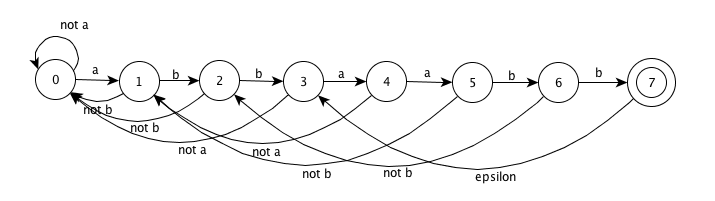
Pseudocode of building the DFA:
for (i = 0; i< n; i ++) {
move[s[i], c] = {
if ( c == b1b2…bn[i] ) {
goto s[i+1]
} else {
goto s[f(i)]
}
}
}
It is obviously that with the known f(n), this DFA can be constructed in O(n) time.
3.6.2
Design finite automata (deterministic or nondeterministic) for each of the languages of Exercise 3.3.5.
3.6.3
For the NFA of Fig. 3.29, indicate all the paths labeled aabb. Does the NFA accept aabb?
Answer
- (0) -a-> (1) -a-> (2) -b-> (2) -b-> ((3))
- (0) -a-> (0) -a-> (0) -b-> (0) -b-> (0)
- (0) -a-> (0) -a-> (1) -b-> (1) -b-> (1)
- (0) -a-> (1) -a-> (1) -b-> (1) -b-> (1)
- (0) -a-> (1) -a-> (2) -b-> (2) -b-> (2)
- (0) -a-> (1) -a-> (2) -b-> (2) -ε-> (0) -b-> (0)
- (0) -a-> (1) -a-> (2) -ε-> (0) -b-> (0) -b-> (0)
This NFA accepts "aabb"
3.6.4
Repeat Exercise 3.6.3 for the NFA of Fig. 3.30.
3.6.5
Give the transition tables for the NFA of:
- Exercise 3.6.3.
- Exercise 3.6.4.
- Figure 3.26.
Answer
Table 1
| state | a | b | ε |
|---|---|---|---|
| 0 | {0,1} | {0} | ∅ |
| 1 | {1,2} | {1} | ∅ |
| 2 | {2} | {2,3} | {0} |
| 3 | ∅ | ∅ | ∅ |
Table 2
| state | a | b | ε |
|---|---|---|---|
| 0 | {1} | ∅ | {3} |
| 1 | ∅ | {2} | {0} |
| 2 | ∅ | {3} | {1} |
| 3 | {0} | ∅ | {2} |
Table 3
| state | a | b | ε |
|---|---|---|---|
| 0 | ∅ | ∅ | {1,2} |
| 1 | {2} | ∅ | ∅ |
| 2 | {2} | ∅ | ∅ |
| 3 | ∅ | {4} | ∅ |
| 4 | ∅ | {4} | ∅ |