Exercises for Section 3.3

3.3.1

Consult the language reference manuals to determine

1. the sets of characters that form the input alphabet (excluding those that may only appear in character strings or comments)
2. the lexical form of numerical constants, and
3. the lexical form of identifiers,

for each of the following languages:

1. C
2. C++
3. C#
4. Fortran
5. Java
6. Lisp
7. SQL

3.3.2

Describe the languages denoted by the following regular expressions:

1. a(a|b)*a
2. ((ε|a)b*)*
3. (a|b)*a(a|b)(a|b)
4. a*ba*ba*ba*
5. !! (aa|bb)*((ab|ba)(aa|bb)*(ab|ba)(aa|bb)*)*

Answer

1. String of a's and b's that start and end with a.
2. String of a's and b's.
3. String of a's and b's that the character third from the last is a.
4. String of a's and b's that only contains three b.
5. String of a's and b's that has a even number of a and b.

3.3.3

In a string of length n, how many of the following are there?

1. Prefixes.
2. Suffixes.
3. Proper prefixes.
4. ! Substrings.
5. ! Subsequences.

Answer

1. n + 1
2. n + 1
3. n - 1
4. C(n+1,2) + 1 (need to count epsilon in)
5. Σ(i=0,n) C(n, i)

3.3.4

Most languages are case sensitive, so keywords can be written only one way, and the regular expressions describing their lexeme is very simple. However, some languages, like SQL, are case insensitive, so a keyword can be written either in lowercase or in uppercase, or in any mixture of cases. Thus, the SQL keyword SELECT can also be written select, Select, or sElEcT, for instance. Show how to write a regular expression for a keyword in a case­ insensitive language. Illustrate the idea by writing the expression for "select" in SQL.

Answer

select -> [Ss][Ee][Ll][Ee][Cc][Tt]

3.3.5

！Write regular definitions for the following languages:

1. All strings of lowercase letters that contain the five vowels in order.
2. All strings of lowercase letters in which the letters are in ascending lexicographic order.
3. Comments, consisting of a string surrounded by / and /, without an intervening */, unless it is inside double-quotes (")
4. !! All strings of digits with no repeated digits. Hint: Try this problem first with a few digits, such as {O, 1, 2}.
5. !! All strings of digits with at most one repeated digit.
6. !! All strings of a's and b's with an even number of a's and an odd number of b's.
7. The set of Chess moves,in the informal notation,such as p-k4 or kbp*qn.
8. !! All strings of a's and b's that do not contain the substring abb.
9. All strings of a's and b's that do not contain the subsequence abb.

Answer

1、

want -> other* a (other|a)* e (other|e)* i (other|i)* o (other|o)* u (other|u)*
other -> [bcdfghjklmnpqrstvwxyz]

2、

a* b* ... z*

3、

\/\*([^*"]*|".*"|\*+[^/])*\*\/

4、

want -> 0|A?0?1(A0?1|01)*A?0?|A0?
A -> 0?2(02)*

Steps:

step1. Transition diagram

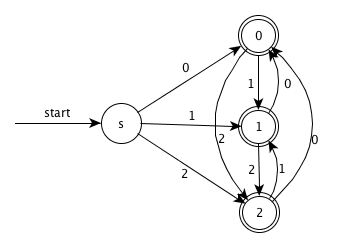
step2. GNFA

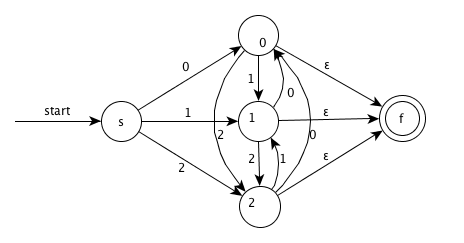
step3. Remove node 0 and simplify

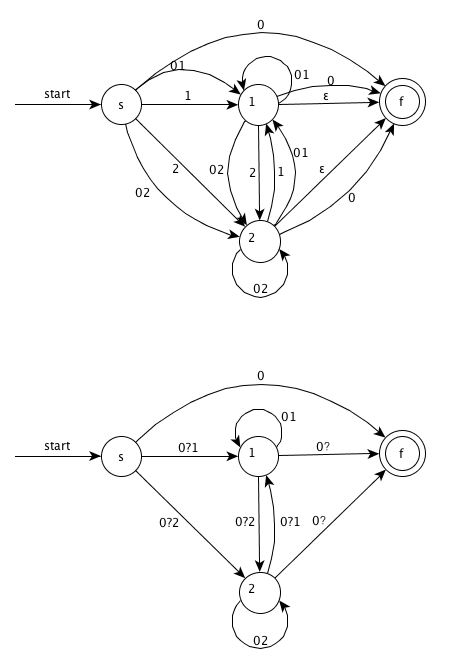
step4. Remove node 2 and simplify

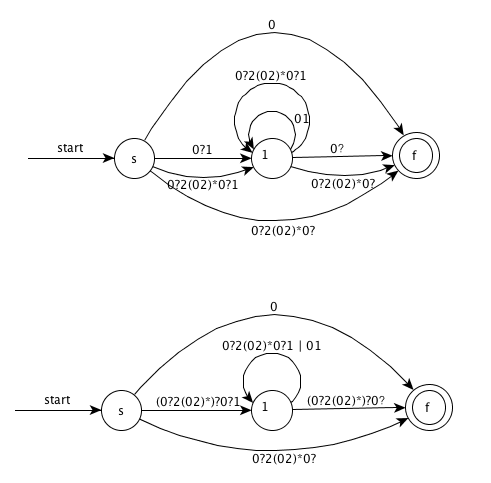
step5. Remove node 1 and simplify

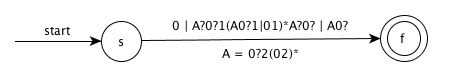
5、

want -> (FE*G|(aa)*b)(E|FE*G)
E -> b(aa)*b
F -> a(aa)*b
G -> b(aa)*ab|a
F -> ba(aa)*b

Steps:

step1. Transition diagram

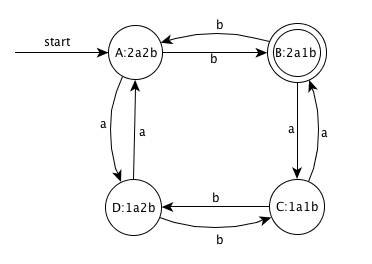
step2. GNFA

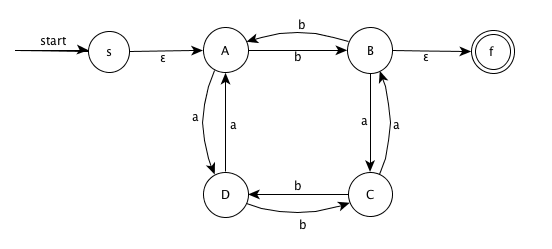
step3. Remove node A and simplify

step4. Remove node D and simplify

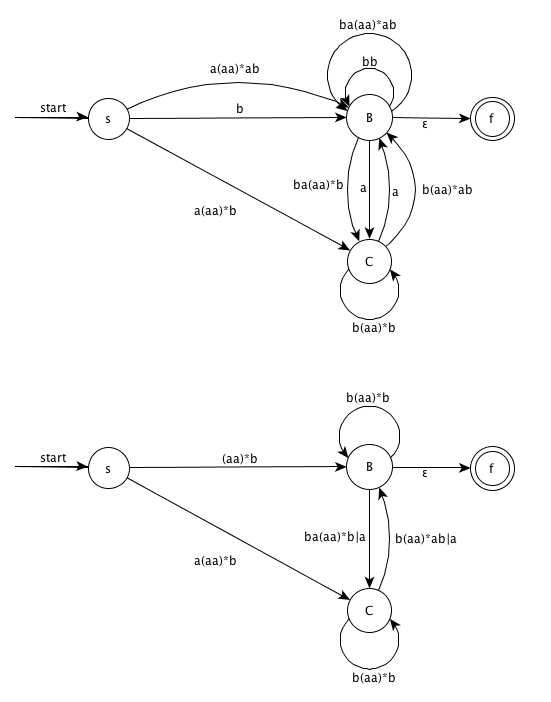
step5. Remove node C and simplify

8、

b*(a+b?)*

9、

b* | b*a+ | b*a+ba*

3.3.6

Write character classes for the following sets of characters:

1. The first ten letters (up to "j") in either upper or lower case.
2. The lowercase consonants.
3. The "digits" in a hexadecimal number (choose either upper or lower case for the "digits" above 9).
4. The characters that can appear at the end of alegitimate English sentence (e.g. , exclamation point) .

Answer

1. [A-Ja-j]
2. [bcdfghjklmnpqrstvwxzy]
3. [0-9a-f]
4. [.?!]

3.3.7

Note that these regular expressions give all of the following symbols (operator characters) a special meaning:

\ " . ^ $ [ ] * + ? { } | /

Their special meaning must be turned off if they are needed to represent themselves in a character string. We can do so by quoting the character within a string of length one or more; e.g., the regular expression "**" matches the string ** . We can also get the literal meaning of an operator character by preceding it by a backslash. Thus, the regular expression \*\* also matches the string **. Write a regular expression that matches the string "\.

Answer

\"\\

3.3.9 !

The regular expression r{m, n} matches from m to n occurrences of the pattern r. For example, a [ 1 , 5] matches a string of one to five a's. Show that for every regular expression containing repetition operators of this form, there is an equivalent regular expression without repetition operators.

Answer

r{m,n} is equals to r.(m).r | r.(m + 1).r | ... | r.(n).r

3.3.10 !

The operator ^ matches the left end of a line, and $ matches the right end of a line. The operator ^ is also used to introduce complemented character classes, but the context always makes it clear which meaning is intended. For example, ^^aeiou*$ matches any complete line that does not contain a lowercase vowel.

1. How do you tell which meaning of ^ is intended?
2. Can you always replace a regular expression using the ^ and $ operators by an equivalent expression that does not use either of these operators?

Answer

1. if ^ is in a pair of brakets, and it is the first letter, it means complemented classes, or it means the left end of a line.